If you wish to color two cells out of the six on a 2 column by 3 row grid, there are precisely 6c2 (15) different permutations. Now let's say you have three different colors and you want to create grids each with 2 cells of each of the three colors and no overlap. The question is:
Is there a set of precisely 15 grids such that all 15 permutations of each of the three colors are represented?
If so, what is it (or what are they)?
And, how do you figure it out?
Operationally, this can be imagined by constructing 15 unique permutations for each color with the remaining spaces empty and then layer one from each of the three sets such that none of the colored spaces overlap and you have no redundancies or left over layers. (see image) You could probably write an algorithm that checks all the combinations, but my sense is that given the number of combinations, an exhaustive search might tax computational time. If I'm correct, 6^15 * some constant, number of calculations. And, it is easy to imagine a slightly expanded grid that is computationally impossible. But, an operational solution is a solution.
So for those of you who like puzzles, here's one that I need help with to create the board pieces for my design. And, help in the form of a possible solution would be greatly appreciated.



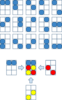

Beautiful. Thanks.
I had an intuition that a solution was possible, but I didn't know for sure. But, you're quick algorithm put it there. Do you think there is more than just one?
Looking at the list of pairs now, it reminds of Sudoku. Each cell must contain 2 of each color and each row must include each of the 15 permutations of RGB.
Thanks again!