Skip to Content
 

need help with a board design puzzle

23 replies [Last post]
Wed, 05/30/2012 - 04:23
jeffinberlin
Offline
Joined: 07/29/2008
Game board puzzle solution as draft for the game board

It's about time I asked for help from this community. It's not that I'm a loner or control freak (well, recovering control freak, perhaps), but I usually prefer to ask for help from the designers and playtesters I see face-to-face on a weekly basis.

However, I have a new game idea I've been working on, and it presents a kind of puzzle that you might be much better at solving than I am. It is in the design of the board and the spaces.

I will not go into the details of the gameplay, because it is irrelevant to this puzzle. Here are the requirements:

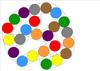
A game board with multiple paths and intersections in which each of the 8 colors of spaces on the paths are equally represented, and each color combination created when 2 spaces lie adjacent appears exactly one time.

For example, a green space is placed next to a blue space, then comes a yellow space, etc. No other place on the game board can have a green space next to a blue space, or a blue space next to a yellow space!

There are 8 colors: green, red, orange, brown, gray, yellow, purple, and blue. This means that each color will combine 7 times--one time each with every other color. For this reason, it seems best to have one 3-way intersection for each color (intersections total). Every color, then, is represented 3 times on the board (one time bordering 3 other colors, and two times bordering 2 colors each).

This means that there are 24 spaces on the board total.

I have already come up with one solution by cutting out domino-like pieces and arranging them until all the above conditions are met. However, I would like to see alternatives, especially those that distribute the colors somewhat equally around the board, if this is possible (so that all the brown spaces are not in the upper half of the board, for example).

If anyone is interested in taking on this challenge, I'm uploading the graphics for the domino-like pieces I used to make my prototype, and also my first attempt at a solution.

If you provide a better solution that I can use, and I can get the game published, I will send you two copies of the game, as well as a "thank you" in the credits.

I hope, though, that the puzzle is a fun game, in and of itself!

Top
Wed, 05/30/2012 - 04:54
#1
jeffinberlin
Offline
Joined: 07/29/2008
more help needed...

How do I upload two more images for this forum post? When I tried to add a second image, it replaced the first.

Thanks!

Top
Wed, 05/30/2012 - 16:36
#2
seo
seo's picture
Offline
Joined: 07/21/2008
This is exactly the kind of

This is exactly the kind of puzzle I love to try solving, so I'll be happy to give it a try. I'll post here my results, if any.

In the meantime, I'll help with the "two or more images in one post" question: try using Markdown with the form: ![Alt text](/path/to/img.jpg)

That way you can include your images like this:

One image: Image 1 and another: Image 2

Edit: Changes your original images for two smaller images also from the BGDF galleries, just because yours were too big to fit in the page layout.

Top
Wed, 05/30/2012 - 23:20
#3
akanucho
Offline
Joined: 11/10/2009
Fantastic problem!

I'll have you know that this problem was stuck in my brain for a good number of hours today. It was wonderful. Thank you, it seems like such a while since I've had such an enjoyable challenge. It took me a long time of trial-and-error before I figured out any sort of system that helped to avoid accidentally duplicating an adjacency. I don't know if you had a system for building your graph, but in case it helps, allow me to share how I generated mine. Please excuse my colors-as-numbers diagram.

     4--5--1
     |  |  |
  2--3  6--7
 /|  |  |  |
6 1  7  4  8
 \|  |  |  |
  8  5  8  5
  |  |  |  |
  3  3  2  2
  |  |  |  |
  6--1--4--7

If you remove the leftmost 6 and the upper-right 1, you'll notice that the top edge of my graph is the numbers 1-8 in order. The bottom edge of the graph (clockwise: 5-2-7-4-1-6-3-8) is also the numbers 1-8, but each successive tile is off by 3, looping around when necessary. It kept alternating even-odd, and in doing so, I made a ring that had all possible even-odd adjacencies exactly once each. The last step was just adding the inner numbers (the 1 and 6 had to remain exterior if the graph was to remain planar) to fill in all the even-even and odd-odd adjacenies.

That's all I could do, and it looks to have kept all the numbers (colors) decently separated (barring 3, sadly, all on the left half). Hope this helps!

Top
Thu, 05/31/2012 - 08:50
#4
gabrielcohn
Offline
Joined: 11/25/2010
I wish I was home...

...b/c at home I have lots of bits lying around to play with to try things out, but, just thinking in my about this, wouldn't a pyramid shape work? I have to run right now, but I'll try to think about it more soon and write back if I have more thoughts. a fun math puzzle!

Top
Thu, 05/31/2012 - 10:57
#5
akanucho
Offline
Joined: 11/10/2009
Oh, this is nice. By

Oh, this is nice. By switching the right-most 2 and 8 (which were each adjacent to both 5 and 7), I was able to shift the exterior 6 and rearrange the interior 2, 4, and 8 to make the graph fit a regular shape. I'm a bit fan of keeping things neat, so to me, this solution is much more attractive.

6--4--5--1
|  |  |  |
2--3  6--7
|  |  |  |
1  7  8  2
|  |  |  |
8  5  4  5
|  |  |  |
3  3  2--8
|  |     |
6--1--4--7

This is the graph as it first came together, but if you prefer more balanced cycle (path loop) lengths, as opposed to the short cycles in the graph's upper corners and the huge one in the center, you can change a few connections, like the 2-3 adjacency in the upper-left could be changed to connecting the 2 and 3 low in the center columns, or the 6 in upper right could connect to the 7 on its other side, or both!

6--4--5--1
|  |  |  |
2  3  6  7
|  | /|  |
1  7/ 8  2
|  |  |  |
8  5  4  5
|  |  |  |
3  3--2--8
|  |     |
6--1--4--7
Top
Thu, 05/31/2012 - 18:48
#6
gabrielcohn
Offline
Joined: 11/25/2010
Another solution

1 2 3 6 4
3 x x x 2
5 4 - 1 6
7 x x x 8
2 8 - 5 1
5 x x x 7
6 7 4 8 3

where - is a connection and x is empty.

Top
Fri, 06/01/2012 - 06:00
#7
nogser
Offline
Joined: 05/31/2012
Another solution

Sorry I don do graphics well but I'll try to depict it after the explanation. If we look at the connection each of the 8 colours needs 1 3 connection. If you create 2 circles one of 8 and an other circle of 16 and place 4 connections between the 2 circles you will have 8 3 space connections. One each for the 8 different colours.

2xxxxxx2xxxxxx2xxxxxx2
xxxxxxxxxx3xxxxxxxxxxx
2xxxxxxxxx3xxxxxxxxxx2
xxxxxxxx2xxx2xxxxxxxxx
xxx3xx3xxxxxx3xxxx3xxx
xxxxxxx2xxx2xxxxxxxxxx
2xxxxxxxxx3xxxxxxxxxx2
xxxxxxxxxx3xxxxxxxxxxx
2xxxxxx2xxxxxx2xxxxxx2

Top
Fri, 06/01/2012 - 06:17
#8
jeffinberlin
Offline
Joined: 07/29/2008
Great work, everyone. Feel

Great work, everyone. Feel free to keep 'em coming!

Top
Sat, 06/02/2012 - 06:45
#9
jeffinberlin
Offline
Joined: 07/29/2008
Thanks

Thanks for trying to solve this puzzle, but this is not a correct solution, as there are only four 3-way connections, which means that 4 of the colors are missing 1 combination (for example, there is no 3-4 adjacency).

In order to work correctly, there needs to be one 3-way intersection for each color (8 total).

Top
Sat, 06/02/2012 - 06:46
#10
jeffinberlin
Offline
Joined: 07/29/2008
akanucho wrote:

akanucho wrote:

6--4--5--1
| | | |
2 3 6 7
| | /| |
1 7/ 8 2
| | | |
8 5 4 5
| | | |
3 3--2--8
| | |
6--1--4--7

I like this one the best so far!

Top
Sun, 06/03/2012 - 11:10
#11
regzr
Offline
Joined: 05/27/2012
24 space 8 color board

Don't know if all the required conditions are met.
But here's one 24 space, 8 color game board.

...........
....6-4....
....l.l....
..4-1.7-3..
..l\.../l..
3-8.5-6.4-2
l...l.l...l
5-2.8-7.6-8
..l/...\l..
..1-5.3-2..
....l.l....
....7-1....
...........

http://www.bgdf.com/node/6619

Top
Sun, 06/03/2012 - 11:54
#12
jeffinberlin
Offline
Joined: 07/29/2008
regzr wrote:Don't know if all

regzr wrote:
Don't know if all the required conditions are met.
But here's one 24 space, 8 color game board.

...........
....6-4....
....l.l....
..4-1.7-3..
..l\.../l..
3-8.5-6.4-2
l...l.l...l
5-2.8-7.6-8
..l/...\l..
..1-5.3-2..
....l.l....
....7-1....
...........

http://www.bgdf.com/node/6619

oooh--a symmetrical one! Very cool!

Top
Sun, 06/03/2012 - 17:57
#13
SLiV
SLiV's picture
Offline
Joined: 10/21/2011
Sixteen fields

Ah, a nice little puzzle. That sure gave me something to do this evening.

After some drawing and redrawing, I've managed to make one with 16 spaces instead of 24, i.e. with every color occuring twice. I don't care much for ascii art, so I took a picture (admittedly a bit blurred):

https://dl.dropbox.com/u/3757149/andere%20uploads/eightcolorgraph.png

Top
Mon, 06/04/2012 - 06:54
#14
55cards
55cards's picture
Offline
Joined: 10/11/2008
Possible graph — no colours (yet)!

Jeff,

This is exactly the sort of design puzzle that I enjoy. Not sure how helpful my partial solution is, but here is a graph that displays the correct connectivity — whether or not is it colourable in the necessary way, I don't know, but I shall certainly try!

(not sure if the markup to embed images will work, but here goes...)

![Uncoloured graph](http://www.bgdf.com/sites/default/files/images/Graph.jpg)

Top
Mon, 06/04/2012 - 15:49
#15
jeffinberlin
Offline
Joined: 07/29/2008
Original!

SLiV wrote:
Ah, a nice little puzzle. That sure gave me something to do this evening.

After some drawing and redrawing, I've managed to make one with 16 spaces instead of 24, i.e. with every color occuring twice. I don't care much for ascii art, so I took a picture (admittedly a bit blurred):

https://dl.dropbox.com/u/3757149/andere%20uploads/eightcolorgraph.png

Ah, very nice variant with more connections and less spaces! Depending on how the game works when playtested, this may be a good alternative!

Top
Mon, 06/04/2012 - 15:53
#16
jeffinberlin
Offline
Joined: 07/29/2008
55cards wrote:Jeff, This is

55cards wrote:
Jeff,

This is exactly the sort of design puzzle that I enjoy. Not sure how helpful my partial solution is, but here is a graph that displays the correct connectivity — whether or not is it colourable in the necessary way, I don't know, but I shall certainly try!

(not sure if the markup to embed images will work, but here goes...)

![Uncoloured graph](http://www.bgdf.com/sites/default/files/images/Graph.jpg)

Yes, I actually enjoy solving the mathematical puzzles that game design creates, as well. Once the vision for the game is there, it's also fun to calculate the number and kinds of cards, board spaces/relationships, dice probabiliites, etc. in order to make a playable prototype.

It has been very fun to see how many different solutions each person has come up with for this simple problem. I now hope that the game I'm using it for works! If not, I'll have to design another game using the same board!

Your board also looks good, with the intersections spaced very well. I'd love to see the color/number relationships.

Top
Tue, 06/05/2012 - 04:54
#17
KAndrw
Offline
Joined: 08/20/2008
This doesn't work, because it

This doesn't work, because it has multiple duplicate connections:

http://i2.photobucket.com/albums/y23/ARowse/IMG_2428.jpg

But I was sure that there would some way of doing it with that structure, which looks quite nice. I wrote a very inefficient program to do a brute-force search for solutions last night, and it had got about 1/8 of the way through the possibilities by this morning, with no success. I'm going to redo it in a more efficient way and try again, but I suspect that it might not actually be solvable.

The program should be able to easily generalise to other structures, though I believe there are about 2 billion (that's trillion, to Americans) combinations of 16 elements, so it could take a while to brute-force!

Top
Thu, 06/07/2012 - 01:31
#18
KAndrw
Offline
Joined: 08/20/2008
Yep - that one's unsolvable,

Yep - that one's unsolvable, which is a great shame.

Brute force won't work so well on the posed problem (one three-link and two two-links per colour), since it has 16!/8! times as many solutions. My program that took ten minutes to exhaust possibility space for this one would take just under ten thousand years to do the other.

A more intelligent program should be able to do it much quicker :)

Top
Thu, 06/07/2012 - 11:20
#19
nogser
Offline
Joined: 05/31/2012
Any more details?

This one keeps throwing shapes that fit the bill description. I have yet to do the colours but two questions keeps coming into my mind? Are you looking for symmetry? What is going on on this board?

Top
Fri, 06/08/2012 - 17:55
#20
SLiV
SLiV's picture
Offline
Joined: 10/21/2011
Interchangeable

KAndrw wrote:
A more intelligent program should be able to do it much quicker :)

Well did you realise that the numbers are completely interchangeable? I.e. that if layout A won't work, then layout A with all 1's and 2's swapped won't work either. That might cut your problem down by a factor 40320 (or more).

But yeah, I reckon it's quite a hassle to figure this one out.

Top
Fri, 06/08/2012 - 18:10
#21
KAndrw
Offline
Joined: 08/20/2008
Yeah - I fixed the

Yeah - I fixed the four-connection nodes with the numbers from 1 to 8, then tried every combination of eight different values in the eight three-connection node.

That came out at 40k (8!) possibilities, which was pretty quick to explore. I was running one test per frame at 60fps, and could easily have sped it up by a factor of 100 or so by doing multiple tests per frame - but then I wouldn't get to watch the numbers flicker all over the place!

With 8 x three-connection nodes and 16 x two-connection nodes (let's call it 3/2/2), there are 16! combinations of the two-connection nodes. That's 20 billion (or trillion, for Americans) combinations, so will take 500 million times as long to exhaustively explore than the 4/3 configuration.

Luckily, you (Sliv) have already proved that at least one 4/3 combination is possible - so I'm still sorely tempted to try a few more layouts, to see if something more symmetrical exists. I'm not going to tackle the 3/2/2 version - it's already been solved by humans here, and I lack the cleverness required to do a non-brute-force search for prettier solutions!

Top
Sun, 06/10/2012 - 17:29
#22
jeffinberlin
Offline
Joined: 07/29/2008
Symmetry is not necessary

I'm not necessarily looking for symmetry on the board. In fact, I am looking for something that looks as organic as possible, which usually means that it is not symmetrical (although I might be able to work with symmetry).

The most important thing is that the colors are dispersed as much as possible (one color should not be located in the same corner of the board) and that there are roughly the same number of spaces between connections (it's better than having long stretches without options of turning one way or the other).

I've posted a graphic of a variation I made on one of the suggestions, which accomplishes this the best so far. I had to switch a few of the connections around so that the lengths of the paths were more similar between the connections.

Thanks!

Top
Tue, 06/12/2012 - 11:38
#23
Orangery
Offline
Joined: 06/06/2012
Fractals

Have you tried looking into fractal structures for an alternative shape... the dragon curve for example?

Top
Syndicate content


forum | by Dr. Radut